Адгезией (от лат. adhaesio — прилипание) называют межфазное взаимодействие между поверхностями конденсированных фаз при их молекулярном контакте. Термин адгезия ввели в 1924 г. Бехольд и Нейман для обозначения специфического молекулярного сцепления в дополнение к господствовавшим тогда представлениям о механическом характере природы склеивания. Работа адгезии Wa — это работа обратимого разрыва адгезионной связи между двумя фазами, отнесенной к единице площади. При этом происходит образование новых поверхностей раздела каждой из этих фаз с воздухом (на это затрачивается энергия (σ1,0 + σ2,0)) и разрушение границы раздела контактировавших фаз (– σ1,2). В результате работа адгезии Wa = σ1,0 + σ2,0 – σ2,1. Это уравнение (уравнение Дюпре) отражает закон сохранения энергии при адгезии.
В отличие от адгезии, которая характеризует взаимодействие между поверхностями разных фаз, когезия отражает связь внутри одной фазы, характеризуя прочность конденсированной фазы и способность тел противодействовать внешнему усилию. Работа когезии определяется затратой энергии на обратимый изотермический разрыв фазы, отнесенной к единице площади. Wк = 2σ1,0 .
Наиболее известные адгезионные эффекты – смачиваемость / несмачиваемость, капиллярность, образование мениска жидкости в узком капилляре, трение покоя двух абсолютно гладких поверхностей.
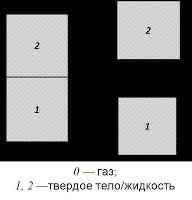
При одновременном контакте жидкости с поверхностью твердого тела или другой жидкости с третьей фазой — газом (воздухом) жидкость может изменять свою форму, собираясь в каплю или растекаясь по поверхности в стремлении уменьшить поверхностную энергию системы. В зависимости от соотношения между силами адгезии между жидкостью и твердым телом и силами когезии внутри жидкости возможны следующие результаты нанесения небольшого количества жидкости на поверхность твердого тела: несмачивание, смачивание и растекание. Угол, образуемый касательной к межфазной поверхности жидкость — воздух, и твердым телом, на которое нанесена жидкость, называют краевым углом смачивания и обозначают через Θ. Тупой угол cos Θ < 0 соответствует несмачиванию (ртуть на стекле, вода на парафине), острый угол cos Θ > 0 — смачиванию; растекание можно интерпретировать как крайний случай смачивания cos Θ = 1, когда капля растекается в тонкую пленку (ртуть на свинце).
Так что же с плащом? Как сделать ткань несмачивемой (гидрофобной)?
Равновесный краевой угол смачивания определяется уравнением Юнга: cos Θ = (σ2,0 – σ2,1)/ σ1,0. Анализ этого уравнения лежит в основе подходов к управлению смачиванием. Для улучшения смачивания водой поверхность модифицируют полярными веществами. Напротив, с целью гидрофобизации на поверхность наносят неполярные вещества или вводят их состав материала. Модифицирование поверхности для регулирования смачивании твердых тел применяется при производстве материалов, используемых во влажной среде (кровельных покрытий, оборудования, красок, тканей). В качестве гидрофобизаторов применяют соли жирных кислот, некоторых металлов (медь, алюминий, цирконий), катионоактивные ПАВ, а также низко- и высокомолекулярные кремнийорганические фторорганические соединения. В практике строительства чаще всего применяются силиконовые гидрофобизаторы на основе алкилсиликонатов калия, алкоксисиланов, гидросодержащих силоксанов, гидроксилсодержащих силоксанов (каучуки).
Капиллярные явления. В тонких трубках (капиллярах) жидкость, смачивающая данную поверхность, образует вогнутый мениск, несмачивающая — выпуклый. В первом случае взаимное притяжение молекул жидкости (когезия) слабее их притяжения молекулами поверхности твёрдого тела (адгезии). Во втором, наоборот, силы когезии преобладают над силами адгезии. Давление паров над вогнутым мениском ниже, а над выпуклым выше, чем над плоской поверхностью жидкости. Этим объясняются, например, явление капиллярной конденсации, капиллярное всасывание жидкости в пористые и волокнистые материалы, поднятие или опускание жидкости по тонким трубкам. Разность давлений, возникающая по обе стороны искривленной поверхности жидкости, называют лапласовым, или капиллярным давлением. Величина лапласова давления зависит от радиуса кривизны поверхности (уравнение Лапласа).
Лапласово давление в капиллярах, радиус которых соизмерим с кривизной поверхности жидкости, является причиной капиллярных явлений, в частности капиллярного поднятия.
Искривление границы раздела фаз в дисперсных системах приводит к изменению условий фазового равновесия. В частности, давление насыщенного пара над выпуклой поверхностью выше, а над вогнутой – ниже, чем над плоской. Уравнение Томсона (Кельвина) связывает давление, при котором пар будет насыщенным по отношению к искривленной поверхности c радиусом кривизны, описывая условия фазовых равновесий в высокодисперсных системах.
