Метод БЭТ сокр., БЭТ (англ. BET) — метод математического описания физической адсорбции основанный на теории полимолекулярной (многослойной) адсорбции.
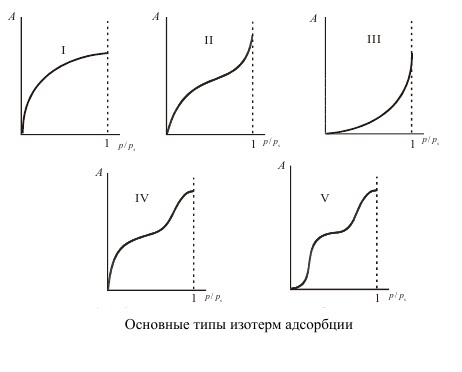
Теория полимолекулярной адсорбции была развита в работах Брунауэра, Эммета и Теллера (БЭТ). В основе этой теории лежит распространение обобщенных представлений локализованного монослоя на полислойную адсорбцию. В теории БЭТ используется предпосылка, что молекулы каждого предыдущего адсорбционного слоя служат активными центрами при образовании последующих слоев. Это предполагает, что емкость каждого слоя одинакова. Считается, что силами взаимодействия между молекулами в каждом адсорбционном слое можно пренебречь (отсутствие латеральных взаимодействий), а молекулы каждого адсорбционного слоя локализованы. Полагается, что адсорбционный потенциал в первом адсорбционном слое значительно выше, чем в других слоях, а начиная со второго адсорбционного слоя он сопоставим с энергией конденсации (изотермы типа II, IV) или для всех слоев одинаков (изотермы III, IV).
Существует несколько методик вывода уравнений изотермы полимолекулярной адсорбции. В работах Брунауэра с сотрудниками использовался кинетический вывод уравнения изотермы полимолекулярной адсорбции. Позднее вывод этого уравнения был осуществлен методом статистической термодинамики.
В оригинальном кинетическом выводе уравнения изотермы адсорбции БЭТ рассматривается равновесие между адсорбционными комплексами различного заполнения. Считается, что на поверхности адсорбента одновременно могут находиться незаполненные активные центры и адсорбционные комплексы, содержащие 1, 2, 3…i, молекул адсорбата, которым соответствует площадь поверхности адсорбентаA0, A1, A2, A3, …Ai.
В 1937 году Брунауэр С., Эммет П. и Теллер Е. вывели уравнение полимолекулярной физической адсорбции, которое описывает зависимость физической адсорбции от величины поверхности:
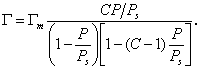
Уравнение известно как простая форма изотермы адсорбции БЭТ. Это уравнение может быть представлено в линейной форме. Обозначим для упрощения Р/РS=Х и разделим на X обе части уравнения:
В такой форме график зависимости должен давать прямую с наклоном С-1/ГmС и отрезком, отсекающим на оси ординат 1/ ГmС .Решение двух численных уравнений позволяет определить постоянную уравнения С, предел адсорбции Гm в монослое и рассчитать удельную активную поверхность Ауд = nmAo = ГmAoNA, где Гm должна быть выражена в моль/г; А0– называют площадью молекулярного сечения адсорбата или чаще – адсорбционной «посадочной площадкой» (этот параметр представляет собой площадь, которую занимает молекула адсорбата в насыщенном мономолекулярном слое).
Температурная зависимость постоянных равновесия K1 и С позволяет определить чистую теплоту адсорбции, так как
где DH1 , DHL – теплота адсорбции в первом адсорбционном слое и теплота конденсации адсорбата.
Если адсорбент пористый и адсорбция идет в результате заполнения мезопор, то уравнение БЭТ принимает вид:
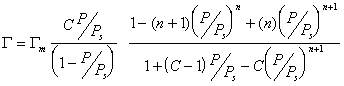
Интересно отметить, что уравнение при n=1 переходит в уравнение Ленгмюра:
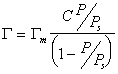
В то время как уравнение БЭТ в простейшей форме может перейти в уравнение Ленгмюра только при дополнительных условиях, что С>>1 и Р/Рs <<1.
Простое уравнение описывает изотермы типов II и III, причем тип изотермы зависит от величины постоянной С, но только изотермы типа II при высоком значении постоянной С дают надежные значения Гm.
Если С>2, то уравнение БЭТ дает изотермы типа II, при С<2 изотерма соответствует типу III. Точка перегиба на изотермах II и IV типов (точка B) соответствует насыщению монослоя. Часто на изотермах типов II и IV после точки B наблюдаются сравнительно длинные линейные участки. В ранних работах Брунауэр предполагал, что насыщению монослоя соответствует точка А на оси ординат (рис. 1, а). Более поздний анализ изотерм и определение предела насыщения монослоя по уравнению позволили установить, что именно ордината точки B соответствует емкости монослоя. В этой связи емкость монослоя можно определить по точке перегиба, не прибегая к более сложной обработке экспериментальных данных. Естественно, что этот перегиб должен быть четко выражен. Если перегиб не выражен четко, то необходимо использовать линейную форму уравнения БЭТ для нахождения предела адсорбции.
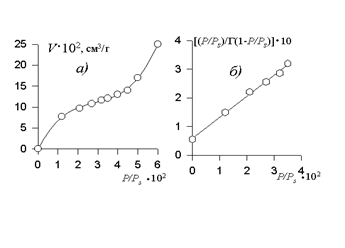
Строго говоря, достаточно надежные данные по емкости монослоя получаются лишь при обработке результатов эксперимента по адсорбции в области малых давлений, где модель полислойной адсорбции БЭТ оказывается справедливой. Часто на линейной изотерме адсорбции наблюдаются два участка – один в области низких относительных давлений, другой — при более высоких давлениях. Для расчетов Гm следует использовать линейный участок при низких давлениях, но только в том случае, если он включает в себя точку В. Чаще всего для определения емкости монослоя используют данные по адсорбции при 0,05< Р/Рs<0,3. Это связано с тем, что при P/Ps<0,05 оказывает влияние неоднородность поверхности, а при Р/Рs>0,3 проявляется латеральное взаимодействие в адсорбционных споях.
Статистико-механическая трактовка полимолекулярной адсорбции и соответствующий вывод уравнения изотермы не позволяют снять указанные выше ограничения.
Кроме того, предпринимались неоднократные попытки модифицировать уравнение БЭТ. Так Андерсон предположил, что от второго до примерно девятого слоев теплота адсорбции отличается от теплоты конденсации на некоторую постоянную величину. Это позволило ввести в простейшее уравнение некоторую постоянную K<1. Уравнение Андерсона имеет вид:
Интересно отметить, что в более поздних работах Брунауэра была получена аналогичная форма уравнения, но вывод его был основан на другой модели, а именно, на предпосылке, что число адсорбционных слоев даже на открытой поверхности при давлении насыщения Р/Рs®1 ограничено (5-6). Такое допущение также noзволяет ввести коэффициент K < 1. При K = 0,79 уравнение (1.3.53) позволяет описать большинство экспериментальных данных для различных адсорбентов и адсорбатов единой кривой (так называемая, единая экспериментальная изотерма адсорбции Шала). Как показал Синг, можно объединить изотермы адсорбции в координатах Q= Г/Гm=f(P/Ps) для широкого набора адсорбентов и адсорбатов, например, изотерму адсорбции азота на кремнеземе с удельной поверхностью от 1 до 200 м2/г, включив в нее изотерму адсорбции на природном кварце и различных образцах непористого и аморфного кремнезема. Такие стандартные изотермы получены и для других систем.
Многочисленные эксперименты на непористых сорбентах показали, что для определения удельной поверхности твердых адсорбентов наиболее удобно простейшее уравнение БЭТ. Для таких целей используют азот, аргон и криптон. Последний, предпочтительнее для адсорбентов с малой величиной удельной активной поверхности.
В методе БЭТ используются следующие допущения:
— поверхность адсорбента однородна;
— взаимодействие адсорбент–адсорбат сильнее, чем адсорбат–адсорбат;
— взаимодействие адсорбированных молекул учитывается только в направлении, перпендикулярном поверхности, и рассматривается как конденсация.
Основной практической целью применения метода БЭТ является нахождение площади поверхности пористого твердого тела. Для этого получают экспериментальную зависимость адсорбции Г от давления Р/Р0 при постоянной температуре (изотерма адсорбции), после чего по уравнению БЭТ вычисляют величину Гm и, затем, число молекул в монослое. Зная площадку, занимаемую одной молекулой, можно рассчитать суммарную площадь поверхности адсорбента любой формы и пористости. Принято считать, что метод БЭТ можно использовать для определения площади поверхности с точностью 5–10% в интервале значений относительного давления (Р/Р0) 0,05–0,35. Для более детального анализа пористой структуры твердого тела (вычисление доли пор различного диаметра в общей пористой структуре) по изотермам адсорбции используют дополнительные расчетные модели.
Источники:
